07-04-2025 - Physics - Scalar Product and Velocity EN]-[IT]

---

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

---

ENGLISH

07-04-2025 - Physics - Scalar Product and Velocity EN]-[IT]
With this post I would like to give a brief instruction about the topic mentioned in the subject
(code notes: X_86-85)

Scalar Product and Velocity

image created with artificial intelligence, the software used is Microsoft Copilot

Introduction
The scalar product in physics is an operation that occurs between two vectors and provides a scalar result, that is, the result is a number and not a vector.
In physics this operation is often linked to the need to determine the work done by a force.
The formula for the scalar product between two vectors A and B is as follows:

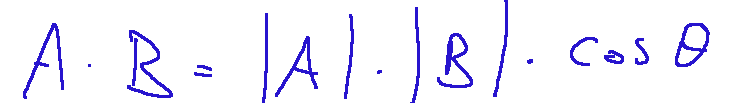
Where:
∣𝐴∣ and ∣𝐵∣ = the lengths (moduli) of the vectors,
cos𝜃 = cosine of the angle 𝜃 between the vectors A and B

We can also write it like this:

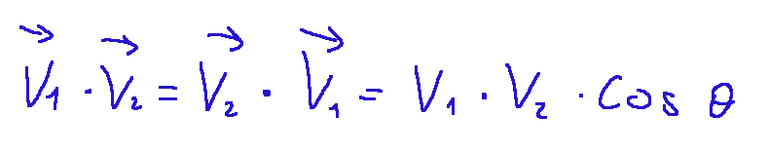
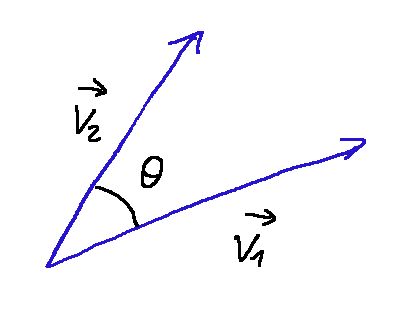
Here is the graphic representation

The properties of the scalar product are:
-Commutative

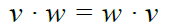
-Distributive


-Homogeneity

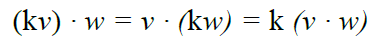
Vector product
Instead, the vector product is an operation between two vectors that returns another vector, also known as the resultant vector.
It is called vector product...

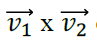
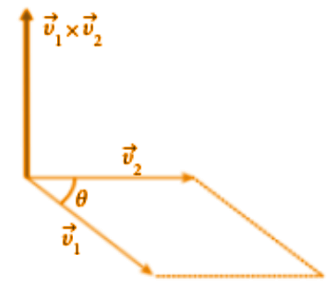
and it is indicated with “x” vector that has:
-modulus equal to v1v2sin𝜃
-direction orthogonal to the plane identified by the 2 vectors v1 and v2
-direction given by the right-hand rule.
Below is an example of an image that graphically reproduces the vector product.

Acceleration and Velocity
When we talk about acceleration and velocity we must clarify the concept of mechanics, dynamics and kinematics.

Mechanics studies the motion of bodies.
It is made up of kinematics and dynamics.
Dynamics deals with the study of motion and its causes.
Kinematics studies motion from a descriptive point of view through the quantities time, position, velocity and acceleration without dealing with the causes of the motion itself. Clarification: Kinematics is the branch of mechanics that describes the motion of a body without analyzing the causes of the motion.
The fundamental physical quantities of kinematics are:
-Space
-Velocity
-Acceleration

The motion of a material point
The description of the motion of a material point is complete when we are able to describe its position as a function of time.

Displacement vector
When the material point moves from A to B in the time interval Δt = t2 – t1, its position vector changes from r1 to r2. This defines the displacement vector which is mathematically represented as follows:

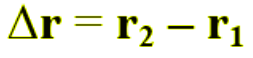
Average velocity

Average velocity represents the speed with which the material point
moves between two positions. It is defined by the ratio represented in the image below.

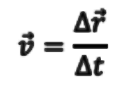
Average acceleration
Average acceleration, in the time interval Δt, is defined as the variation of velocity over time.

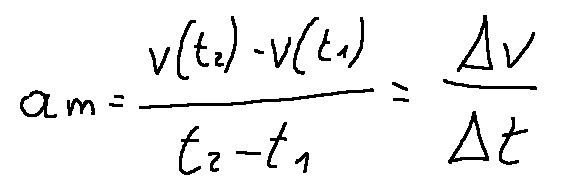
We can also describe average acceleration like this. Average acceleration is a physical quantity that measures the change in velocity of an object with respect to the time in which this change occurs. It is calculated as the ratio between the change in velocity (Δ𝑣) and the time interval (Δ𝑡) during which the change occurs.

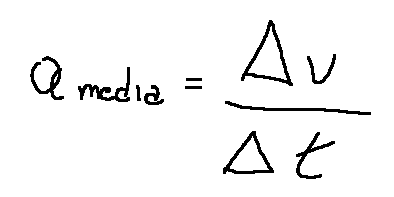
Instantaneous acceleration
Instantaneous acceleration is defined as the limit of the incremental ratio between the change in velocity and the interval of time.
Below is its mathematical expression.

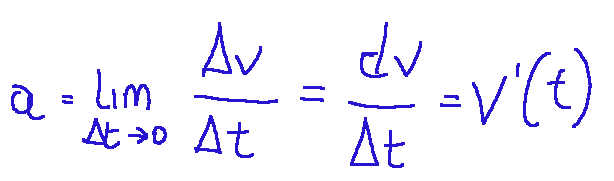
Instantaneous acceleration at a certain instant is the slope of the tangent line to the curve at that instant.

Instantaneous acceleration also corresponds to the derivative of velocity with respect to time, or the second derivative of displacement with respect to time.

The derivative is a tool in differential calculus that is used to study how a function changes in relation to an infinitesimal variation of its independent variable. In other words, it measures the rate of change of a function.

Why is it important in the study of velocities and accelerations?
In physics, the derivative of position with respect to time gives velocity, and the derivative of velocity gives acceleration.

Conclusions
Vectors and acceleration are closely related in physics, since acceleration is a vector quantity.

Question
As written in this article, a vector quantity is a physical quantity that requires three fundamental pieces of information to be described: magnitude, direction and verse. We said that acceleration is a vector quantity, did you know that force is also a vector quantity?

---

---

ITALIAN

07-04-2025 - Fisica - Prodotto scalare e velocità EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_86-85)

Prodotto scalare e velocità

immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot

Introduzione
Il prodotto scalare in fisica è un operazione che avviene tra due vettori e fornisce un risultato scalare, cioè il risultato è un numero e non un vettore.
In fisica questa operazione è spesso legata alla necessità di determinare il lavoro fatto da una forza.
La formula del prodotto scalare tra due vettori A e B è la seguente:

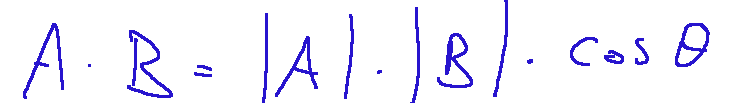
Dove:
∣𝐴∣ e ∣𝐵∣ = le lunghezze (moduli) dei vettori,
cos𝜃 = coseno dell'angolo 𝜃 tra i vettori A e B

Possiamo anche scriverlo così:

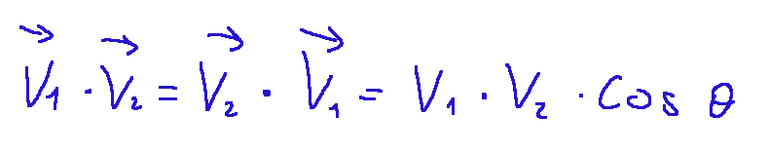
Qui di seguito la rappresentazione grafica

Le proprietà del prodotto scalare sono:
-Commutativa

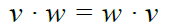
-Distributiva

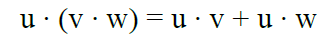
-Omogeneità

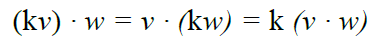
Prodotto vettoriale
Invece il prodotto vettoriale è un'operazione tra due vettori che restituisce un altro vettore, noto anche come vettore risultante.
Si definisce prodotto vettoriale...

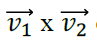
e si indica con “x” vettore che ha:
-modulo pari a v1v2sen𝜃
-direzione ortogonale al piano individuato dai 2 vettori v1 e v2
-verso dato dalla regola della mano destra.
Qui di seguito un esempio di un'immagine che riproduce graficamente il prodotto vettoriale.

Accelerazione e Velocità
Quando parliamo di accelerazione e velocità dobbiamo chiarire bene il concetto di meccanica, dinamica e cinematica.

La meccanica studia il moto dei corpi.
Essa è costituita dalla cinematica e dalla dinamica.
La dinamica si occupa dello studio del moto e delle sue cause.
La cinematica studia il moto da un punto di vista descrittivo tramite le grandezze tempo, posizione, velocità ed accelerazione senza occuparsi delle cause del moto stesso. Precisazione: La cinematica è il ramo della meccanica che descrive il moto di un corpo senza analizzare le cause del movimento.
Le grandezze fisiche fondamentali della cinematica sono:
-Spazio
-Velocità
-Accelerazione

Il moto di un punto materiale
La descrizione del moto di un punto materiale è completa quando siamo in grado di descriverne la posizione in funzione del tempo.

Vettore spostamento
Quando il punto materiale si muove da A a B nell’intervallo di tempo Δt = t2 – t1, il suo vettore posizione cambia da r1 ad r2. Si definisce in questo modo il vettore spostamento che è rappresentato matematicamente così:

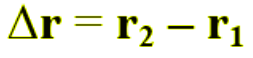
Velocità media

La velocità media rappresenta la rapidità con cui il punto materiale
si sposta tra due posizioni. Viene definita dal rapporto rappresentato nell'immagine qui sotto riportata.

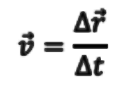
Accelerazione media
Si definisce accelerazione media, nell’intervallo di tempo Δt, la variazione della velocità nel tempo.

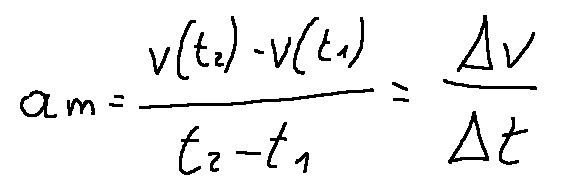
Possiamo descrivere l'accelerazioe media anche così. L'accelerazione media è una grandezza fisica che misura il cambiamento della velocità di un oggetto rispetto al tempo in cui avviene questo cambiamento. È calcolata come il rapporto tra la variazione di velocità (Δ𝑣) e l'intervallo di tempo (Δ𝑡) durante il quale il cambiamento si verifica.

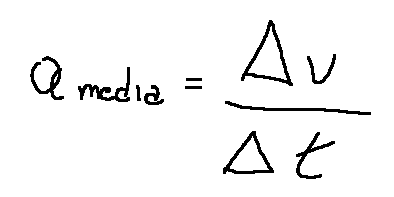
Accelerazione istantanea
L’accelerazione istantanea viene definita come il limite del rapporto incrementale tra la variazione di velocità e l’intervallo fi tempo.
Qui di seguito la sua espressione matematica.

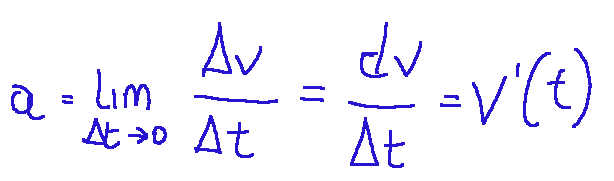
L’accelerazione istantanea in un certo istante è la pendenza della retta tangente alla curva in quell’istante.
L’accelerazione istantanea corrisponde anche alla derivata della velocità rispetto a l tempo ovvero la derivata seconda dello spostamento rispetto a tempo.

La derivata è uno strumento del calcolo differenziale che serve a studiare come cambia una funzione in relazione a una variazione infinitesimale della sua variabile indipendente. In altre parole, misura la velocità di variazione di una funzione.

Perché è importante negli studi delle velocità e delle accelerazioni?
In fisica, la derivata della posizione rispetto al tempo dà la velocità, e la derivata della velocità dà l'accelerazione.

Conclusioni
I vettori e l'accelerazione sono strettamente connessi nella fisica, poiché l'accelerazione è una grandezza vettoriale.

Domanda
Come è scritto in questo articolo una grandezza vettoriale è una grandezza fisica che per essere descritta necessita di tre informazioni fondamentali: modulo, direzione e verso. Abbiamo detto che l'accelerazione è una grandezza vettoriale, lo sapevate che anche la forza è una grandezza vettoriale?

THE END